Main Index Number Theory Arithmetics Multiplication
Subject Index
comment on the page

Peasant multiplication

A variant of multiplication was used in old Egypt already in 18th century BC. Its advantage is that it does not require the knowledge of the whole multiplication table. To its realization only knowledge of addition, multiplication by 2 (doubling) and division by 2 (halving) is required. The doubling can be realized very simply by copying symbols and normalizing by a carrying process if any group of symbols is larger than 9 in size, similarly the halving. ¹  From that reason it is suitable for uneducated people. It was also used in Europe, but with increase of the educational level it was forgotten in the meantime. In 19th century it was rediscovered in Russia where it survived in daily usage and it was mostly used by uneducated peasants, and from that reason it is also called Russian (peasant) multiplication.  

For instance you would like to multiply by . Two columns are set up as shown below:  you start with both factors in the first row. In the next row you double the value of and half the value of . If is odd the remainders are ignored. Simultaneously you can, however, mark the rows with odd , that is where the division by 2 has a remainder. This will be repeated until the number in halves column is reduced to . Then the sum of marked numbers in the doubles column gives the product .

The idea behind the scene is the conversion of one of the factors (more precisely of the multiplier) into binary form by repeated dividing by two and keeping track of the remainder . Actually reading the remainders from bottom to top we get the binary form of the halved factor. In our case , i.e.   and the distributive law finishes the proof of the correctness of the procedure:

Another proof of the correctness is as follows:

• we start to compute . When the factor which is halved is even, then the identity shows that the product of the number in the row equals that of the numbers in the preceding row,  
• when the halved number is odd then the identity shows that the product of the numbers in the row decreases by compared to the final product . Consequently, the product we get when to the final double we add all the odd halves.     

If is the smallest of both factors, then the number of rows is clearly given by the smallest satisfying the inequality , i.e. .  

To compute more examples go to .

The change from base ten to base two was more visible in the following form of the above multiplication used by ancient Egyptians. They were unaware of such concepts but the principles could be applied using much simpler methods. The technique is known to us from the Moscow   and Rhind ²   Mathematical Papyri   written in the seventeenth century B.C.

Ancient Egyptian multiplication method for multiplying two numbers uses only the ability to multiply and divide by 2, and to add .  From our point of view they found the binary decomposition of the multiplicand using the idea of finding the powers of two which make it up. They proceeded in such a way that they initially find the largest power of two less than or equal to the multiplicand, then they subtract it out and repeat until nothing remained. Instead of our multiplication table they used tables of a great number of powers of two if necessary and so as they were not to obliged to recalculate them each time during the multiplications.

The Egyptians has the form of  a table consisting of two columns in the following way (the rows marked with the sign  + are those powers of 2, which make up the multiplier):

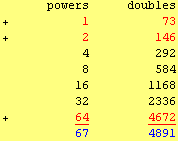
Egyptians also used other methods for multiplication.

To compute more examples go to .

To read more about the Ancient Egypt culture visit  .

The Russian multiplication is also called Ethiopian. According to some theories the ancient Egyptians migrated to Egypt from the once fertile Sahara region of Africa. These early inhabitants of Africa were referred to as Ethiopians .

Notes

Cite this web-page as: