## From perceptron ## to deep neural networks <br> Petra Vidnerová Ústav informatiky, AV ČR

### Intro <img src="./fig/square.png" width="35%" style="float:left; border: none"/> <div > <small> + Artificial inteligence + Machine learning + Statistics + Neural networks + Kernel methods + Meta-learning + Evolutionary algorithms + Learning theory + ... </small> </div>

<img src="./fig/ml-stat-cs.png" width="45%"/>

### Outline + Neural networks overview - First perceptron model - MLP, RBF networks, kernel methods - Deep and convolutional networks + Our work - quantile estimation by neural networks - adversarial examples

### Looking back at history ...  **1957 Perceptron** + Frank Rosenblatt introduced a model of neuron with supervised learning algorithm. + First neural computer for pattern recognition, images 20x20, Mark 1 Perceptron.

### Perceptron model <img src="./fig/single_perceptron.png" width="40%"/> <img src="./fig/neuron.jpg" width="35%"/> + inputs, weights, bias, potencial + implement only linearly separable functions `$$ y = \begin{cases} 1 & \text{if } \sum_{i=1}^n w_i x_i - \theta \geq 0 \\ 0 & \text{else} \end{cases}$$`

### Perceptron learning algorithm **Problem**: inputs `$x_1, \ldots, x_n$`; output `0/1` 

### Geometric interpretation <img src="./fig/geometry.png" width="35%" style="float:left"/> <div><small> `$ x \in P$` we need `$ {\bf wx} \gt 0$` i.e. we need angle between `${\bf w}$` and `${\bf x} < 90^\circ$` `$\cos \alpha = \frac{{\bf w}{\bf x}}{||{\bf w}||\cdot||{\bf x}||}$` `${\bf w}{\bf x} \gt 0 \rightarrow \cos \alpha \gt 0 \rightarrow \alpha \lt 90^\circ$` </small></div>

### Explanation 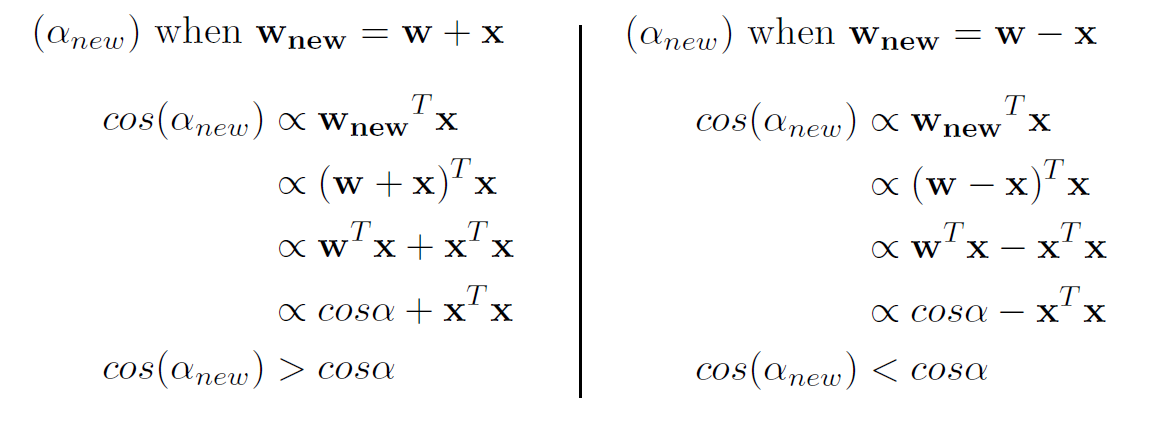 Was proven that the algorithm converges. See for example [Michael Collins proof](http://www.cs.columbia.edu/~mcollins/courses/6998-2012/notes/perc.converge.pdf).

### Problem XOR  **1969 Minsky** Limitation of perceptron. Cannot solve the problem XOR. Start of AI winter.

### Multi-layer perceptrons (MLP) <img src="./fig/mlp.png" width="50%"/> **1986 Backpropagation (Rumelhart et al and others)** Least square method for learning neural networks with multiple layers.

### Back propagation <img src="./fig/gradient.png" width="30%"/> <span style="float: right; padding: 10px"> <small> <ul> <li> gradient learning of neural networks <br> by means of backward error propagation </li> <li> optimisation of error/loss function </li> <li> how many layers we need (theory) </li> <li> how many layers we should use (practice) </li> <li> gradient descent algorithm </li> </ul></small> </span> <img src="./fig/learningrule.png" width="30%"/> <img src="./fig/gradient2.png" width="30%" />

### Derivatives <small> $$ \begin{eqnarray} E = \sum_{k=1}^N E_k & \qquad & \triangle w_{ij} = -\varepsilon \frac{\delta E}{\delta w_{ij}} \\ \frac{\delta E}{\delta w_{ij}} = \sum_{k=1}^N \frac{\delta E_k}{\delta w_{ij}}& & \frac{\delta E_k}{\delta w_{ij}} = \frac{\delta E_k}{\delta o_i} \frac{\delta o_i}{\delta \xi_i} \frac{\delta\xi_i}{\delta w_{ij}} \\ o_{ij} = \varphi (\sum_{k=1}^p (w_{ijk} x_{k} - \theta_{ij})) &\qquad & \varphi(z) = \frac{1}{1 + e^{-z}}, \frac{\delta\varphi(z)}{\delta z} = \varphi(z) (1-\varphi(z)) \\ \frac{\delta E_k}{\delta w_{ij}} = \frac{\delta E_k}{\delta o_i} o_i (1 - o_i)o_j & &\\ \end{eqnarray} $$ </small> If $o_i$ is the output neuron: $ \frac{\delta E_k}{\delta o_i} = y_i - d_k $ If $o_i$ is an hidden neuron: $ \frac{\delta E_k}{\delta o_i} = \sum_{r \in i^{\rightarrow}} \frac{\delta E_k}{\delta o_r} o_r (1-o_r) w_{ir}$

### Loss function and regularization <small> + Mean square error (MSE): $$E = \frac{1}{N} \sum_{k=1}^N (f(x_k) - d_k)^2q$$ + Function approximation - ill posed problem 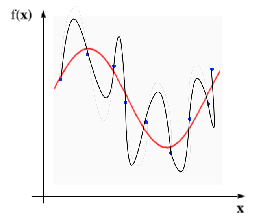 + Add regularization, weight decay </small>

### Loss function and regularization <small> + Mean square error (MSE): <div style="color:red"> $$E = \frac{1}{N} \sum_{k=1}^N (f(x_k) - d_k) + \gamma \Phi[f] $$ </div> + Function approximation - ill posed problem  + Add regularization, weight decay </small>

### RBF Networks 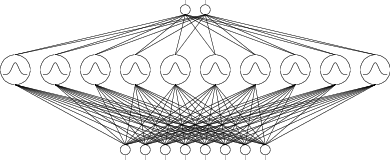 <small> + originated in 1980s, function approximation + network with one hidden layer + local units + alternative to perceptron </small> RBF unit: $y(\vec{x}) = \varphi(\frac{||\vec{x}-\vec{c}||}{b}) = e^{-(\frac{||\vec{x}-\vec{c}||}{b})^2}$ Network function: $ f(\vec{x}) = \sum_{j=1}^h w_j \varphi(\frac{||\vec{x}-\vec{c}||}{b})$

### Two spirals problem <img src="./fig/2spirals.png" width="29%"/> <img src="./fig/2sp70output.png" width="29%"/> <img src="./fig/rbf_function.png" width="29%" style="border:0"/> Difficult problem for linear separation.

### Kernel methods (SVM) <img src="./fig/googleml.png" width="30%"/> <img src="./fig/googlenn.png" width="30%"/> <img src="./fig/googlesvm.png" width="30%"/> In '90s kernel methods and SVMs were very popular.

### Mapping to the feature space <img src="./fig/feature_space.png" width="60%"/> Choose a mapping to a (high dimensional) dot-product space - feature space.

### Mercer's condition and kernels <div style="text-align:left"><b>Mercer theorem:</b></div> <small> If a symmetric function $K(x, y)$ satisfies $$ \sum_{i,j = 1}^M a_i a_j K(x_i, x_j) \gt 0$$ for all $M \in {\mathbf N}, x_i$ and $a_i \in {\mathbf R}$, there exists a mapping function $\phi$ that maps $x$ into the dot-product feature space and $$ K(x, y) = \langle \phi(x), \phi(y) \rangle$$ and vise versa. Functio $K$ is called <b>kernel</b>. </small>

Support vector machine

Looking for a separating hyperplane with the maximal margin.

### Convolutional Networks <img src="./fig/lenet.png" width="70%"/> **1994 LeNet5 (Yann LeCun)** Convolutional layers for feature extraction. Subsampling layers (max-pool layers).

### Descrete convolution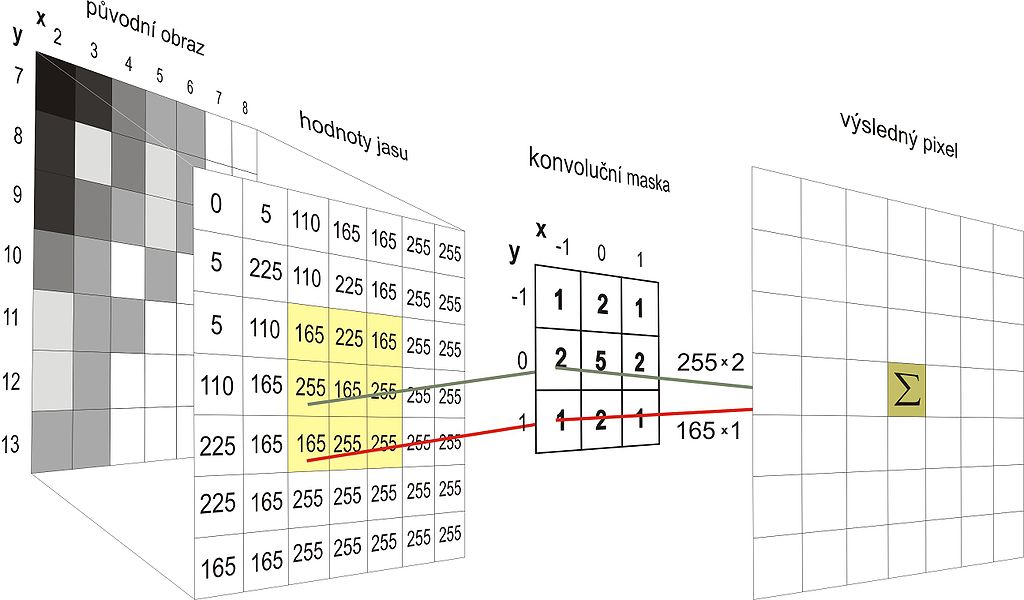 

### Edge detection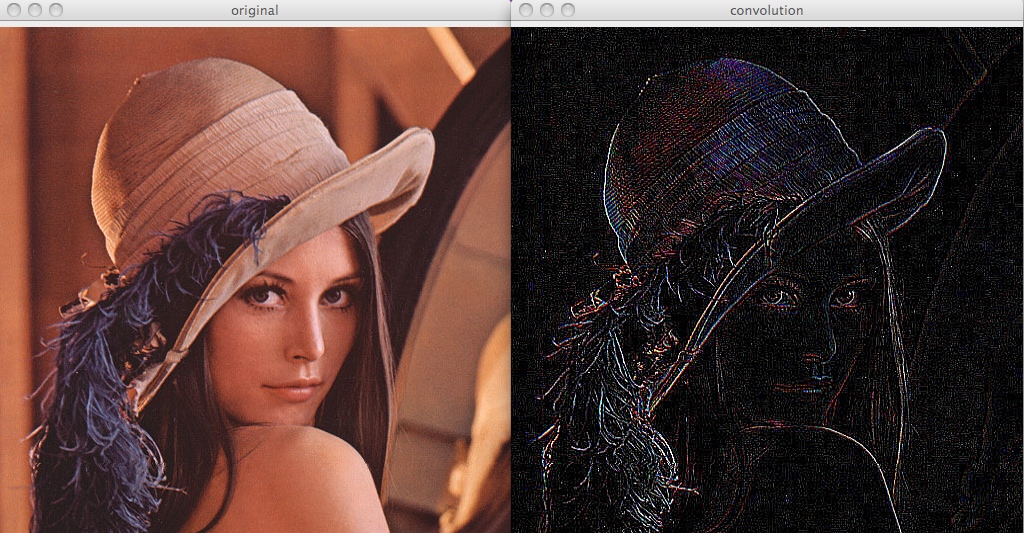 

### LeNet network Example 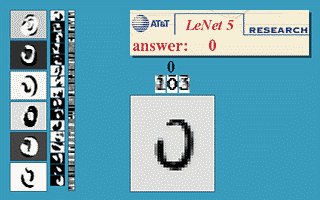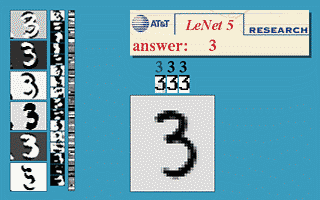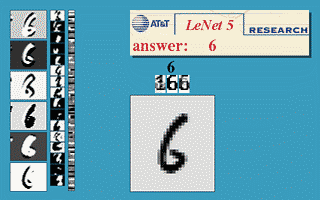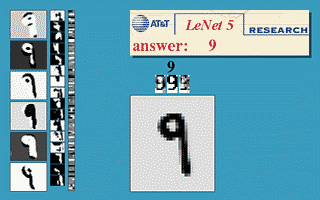 Was applied in several banks for recognition of numbers on cheques.

### Deep neural networks <img src="./fig/gpu.png" width="70%" style="border:0"/> **Bengio, Hinton, LeCun (2009)** Big data + GPUs/TPUs. Learning with millions of neurons. New architectures available for computer vision, video processing, NLP.

<img src="./fig/ai_timeline.png" width="50%"/> ### Advances in deep learning ... + ReLU activation units (vanishing gradient problem) <img src="./fig/sigmoid_relu.png" width="50%" style="text-align:center"/>

### Advances in deep learning + Dropout - type of regularization, as ansamble + Learning with mini-batches + Convolutional layers - adaptive preprocessing <img src="./fig/ml_dl_difference2.png" width="50%"/> + Transfer learning + Float types with lower numbers of bits (8bits) + Missing interpretation

# Our Work

### Quantile Estimation 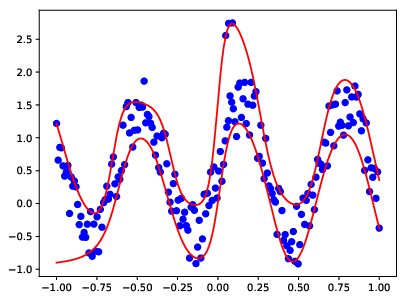 + instead of mean trend predict the desired quantile + joint work with Jan Kalina

### Quantile Estimation + data points $ (x_i, y_i), i = 1, \ldots, N$ + for each $i$ resudial $ \xi_i = y_i - f(x_i) $ + MSE: $$E = \sum_{k=1}^N \xi_i^2 = \sum_{k=1}^N \rho(\xi_i) $$ $$ \rho(z) = z^2$$

### Quantile Estimation + modify a loss function (R. Koenker) `$$ \rho(z) = \begin{cases} \tau |x|, & \text{if } x \gt 0 \\ (1-\tau) |x|, & \text{else}\\ \end{cases} $$` <img src="./fig/quantile_loss.png" width="40%"/>

### Quantile Estimation - toy example Simple MLP. <img src="./fig/mlp_0.1_0.9.png" width="30%"/> <img src="./fig/mlp_0.2_0.8.png" width="30%"/> <img src="./fig/mlp_0.3_0.7.png" width="30%"/> $ \tau = 0.1 \text{and } 0.9$ (left) $ \tau = 0.2 \text{and } 0.8$ (center) $ \tau = 0.3 \text{and } 0.7$ (right)

### Quantile Estimation - toy example Simple MLP. <img src="./fig/mlp_0.9_0.1.png" width="30%"/> <img src="./fig/mlp_0.8_0.2.png" width="30%"/> <img src="./fig/mlp_0.7_0.3.png" width="30%"/> $ \tau = 0.1 \text{and } 0.9$ (left) $ \tau = 0.2 \text{and } 0.8$ (center) $ \tau = 0.3 \text{and } 0.7$ (right)

### Network robustification Simple RBF. Data above and bellow quantiles are omitted. <img src="./fig/rbf_plain.png" width="40%"/> <img src="./fig/rbf_restricted.png" width="40%"/>

### Adversarial Examples <img src="./fig/breakconv_2.png" width="60%"/> **2015 Goodfellow** <small> + applying an imperceptible non-random pertrubation to an input image, it is possible to arbitrarily change the machine learning model prediction + for a human eye, adversarial examples seem close to the original examples + a **security flaw** in a classifier </small>

### Crafting adversarial examples <small> + optimisation problem, $w$ is fixed, $x$ is optimised + minimize $||r||_2$ subject to $f(x+r) = l$ and $(x+r) \in \langle 0, 1 \rangle^m$ + a box-constrained L-BFGS <hr> + **gradient sign method** - adding small vector in the direction of the sign of the derivation + we can linearize the cost function around $θ$ and obtain optimal perturbation $$ \eta = \varepsilon \text{sign}(\Delta_x J(\theta, x, y))$$ </small>

### Crafting adversarial examples II. <small> + **adversarial saliency maps** -- identify features of the input that most significantly impact output classifications (Papernot, 2016) + motivation: output function (left), forward derivation (right) <img src="./fig/fceand.png" width="35%"/> <img src="./fig/derivand.png" width="35%"/> <img src="./fig/smap.png" width="20%"/> + misclasify $X$ such that it is assigned a target class $t \neq label(X)$, $F_t(X)$ must increase, while $F_j(X), j \neq t$ decrease `$$ S(X,t)[i] = \begin{cases} 0 \text{ if }\frac{\delta F_t(X)}{\delta X_i} < 0 \text{ or } \sum_{j \neq t} \frac{\delta F_j(X)}{\delta X_i} > 0 \\ \frac{\delta F_t(X)}{\delta X_i} |\sum_{j \neq t} \frac{\delta F_j(X)}{\delta X_i}| \text{ otherwise} \end{cases}$$` </small>

### FGSM vs. Saliency maps <img src="./fig/legitimate.png" width="70%"/><br> Crafted by FGSM: <img src="./fig/fgsm.png" width="70%"/><br> Crafted by saliency maps: <img src="./fig/saliency.png" width="70%"/>

### Attack taxonomy 

### Results on GTSRB <img src="./fig/gtsrb.png" width="60%"/>

### Genetic Crafting Algorithm + To obtain an adversarial example for the trained machine learning model, we need to optimize the input image with respect to model output. + For this task we employ a GA – robust optimisation method working with the whole population of feasible solutions. + The population evolves using operators of selection, mutation, and crossover. + The ML model and the target output are fixed.

### Black-box approach + genetic algorithms to generate adversarial examples + machine learning method is a blackbox + applicable to all methods without the need to acess models parameters (weights) <img src="./fig/model_ga_adv.png" width="45%"/>

### Results for different ML models <img src="./fig/adversary_9.png" width="60%"/> <img src="./fig/adversary_svm_9.png" width="60%"/>

 ### Questions?