


Next: Conclusion
Up: On entropy rates of
Previous: Results
Solutions of dynamical systems in the vicinity of bifurcation may
have longer transient times than solutions in other states.
Could the increased transient time be the reason for
the digressions from the one-to-one functional
dependence of the GPER on the KSE/LE? Using the logistic map in the range of the parameter a
considered in Fig. 2d-f, we have studied variances of the
GPER estimates (using the 15 realizations of 16k time series)
as well as variances of the LE estimates,
after skipping out different numbers of initial iterations
considered as the transient time.
In this case we
used 15 LE estimates from 20,000 iterations each
(unlike in the previous section, where the LE estimates
from whole 300,000 iterations were used).
The SD (standard deviations, square roots of the variances)
of the GPER (Fig. 4a,c,e) and LE (Fig. 4b,d,f) estimates
as functions of the parameter a are plotted
in Fig. 4.
When no transient iterations were omitted
and the computation of the GPER and the LE started at the beginning
of the iteration,
the variances of the GPER and LE estimates
are very large due to the transients (Fig. 4a,b, note different scales).
Starting the LE/GPER estimation after
skipping
hundred thousand
Using the logistic map in the range of the parameter a
considered in Fig. 2d-f, we have studied variances of the
GPER estimates (using the 15 realizations of 16k time series)
as well as variances of the LE estimates,
after skipping out different numbers of initial iterations
considered as the transient time.
In this case we
used 15 LE estimates from 20,000 iterations each
(unlike in the previous section, where the LE estimates
from whole 300,000 iterations were used).
The SD (standard deviations, square roots of the variances)
of the GPER (Fig. 4a,c,e) and LE (Fig. 4b,d,f) estimates
as functions of the parameter a are plotted
in Fig. 4.
When no transient iterations were omitted
and the computation of the GPER and the LE started at the beginning
of the iteration,
the variances of the GPER and LE estimates
are very large due to the transients (Fig. 4a,b, note different scales).
Starting the LE/GPER estimation after
skipping
hundred thousand initial iterations led to decrease of the variance of the estimates
-- SD of LE (Fig. 4d) decreased several times and
SD of GPER (Fig. 4c)
decreased one order of magnitude.
The number of the ``transient iterations'', i.e.
the number of the
skipped initial iterations
was further increased through
initial iterations led to decrease of the variance of the estimates
-- SD of LE (Fig. 4d) decreased several times and
SD of GPER (Fig. 4c)
decreased one order of magnitude.
The number of the ``transient iterations'', i.e.
the number of the
skipped initial iterations
was further increased through 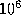 ,
, 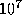 ,
,  , up
to one billion (
, up
to one billion ( 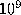 , Fig. 4e,f), however, no further changes in the
variance of the estimates were observed.
Therefore we could conclude that omitting
, Fig. 4e,f), however, no further changes in the
variance of the estimates were observed.
Therefore we could conclude that omitting  initial iterations
was enough for transients to disappear and for the system to converge
to the attractor in all considered states (all considered values of
the parameter a). Larger variances in the vicinity of bifurcations
are probably due to typical behaviour (fluctuations) of systems in critical
states. Note that the intervals of the increased variance of the GPER are limited to the
points located immediately before and after bifurcations, while
the variance of the LE rises gradually in wider intervals surrounding
the bifurcations.
This phenomenon is illustrated in detail in Fig. 5,
where the LE, the GPER
and their variances are plotted as functions of the parameter a,
depicting one of the bifurcations into periodic states.
initial iterations
was enough for transients to disappear and for the system to converge
to the attractor in all considered states (all considered values of
the parameter a). Larger variances in the vicinity of bifurcations
are probably due to typical behaviour (fluctuations) of systems in critical
states. Note that the intervals of the increased variance of the GPER are limited to the
points located immediately before and after bifurcations, while
the variance of the LE rises gradually in wider intervals surrounding
the bifurcations.
This phenomenon is illustrated in detail in Fig. 5,
where the LE, the GPER
and their variances are plotted as functions of the parameter a,
depicting one of the bifurcations into periodic states.
The results presented above suggest that the discrepancies
in the functional relation between the
GPER and the KSE (LE) at the vicinity of bifurcations
are not due to transients, but
probably
due to critical behaviour of the system
near a bifurcation point.
Therefore the linear description (based on the spectral density) is inadequate for
systems in critical states.



Next: Conclusion
Up: On entropy rates of
Previous: Results
Milan Palus
Mon Dec 16 09:47:50 EST 1996
 Using the logistic map in the range of the parameter a
considered in Fig. 2d-f, we have studied variances of the
GPER estimates (using the 15 realizations of 16k time series)
as well as variances of the LE estimates,
after skipping out different numbers of initial iterations
considered as the transient time.
In this case we
used 15 LE estimates from 20,000 iterations each
(unlike in the previous section, where the LE estimates
from whole 300,000 iterations were used).
The SD (standard deviations, square roots of the variances)
of the GPER (Fig. 4a,c,e) and LE (Fig. 4b,d,f) estimates
as functions of the parameter a are plotted
in Fig. 4.
When no transient iterations were omitted
and the computation of the GPER and the LE started at the beginning
of the iteration,
the variances of the GPER and LE estimates
are very large due to the transients (Fig. 4a,b, note different scales).
Starting the LE/GPER estimation after
skipping
hundred thousand
Using the logistic map in the range of the parameter a
considered in Fig. 2d-f, we have studied variances of the
GPER estimates (using the 15 realizations of 16k time series)
as well as variances of the LE estimates,
after skipping out different numbers of initial iterations
considered as the transient time.
In this case we
used 15 LE estimates from 20,000 iterations each
(unlike in the previous section, where the LE estimates
from whole 300,000 iterations were used).
The SD (standard deviations, square roots of the variances)
of the GPER (Fig. 4a,c,e) and LE (Fig. 4b,d,f) estimates
as functions of the parameter a are plotted
in Fig. 4.
When no transient iterations were omitted
and the computation of the GPER and the LE started at the beginning
of the iteration,
the variances of the GPER and LE estimates
are very large due to the transients (Fig. 4a,b, note different scales).
Starting the LE/GPER estimation after
skipping
hundred thousand initial iterations led to decrease of the variance of the estimates
-- SD of LE (Fig. 4d) decreased several times and
SD of GPER (Fig. 4c)
decreased one order of magnitude.
The number of the ``transient iterations'', i.e.
the number of the
skipped initial iterations
was further increased through
initial iterations led to decrease of the variance of the estimates
-- SD of LE (Fig. 4d) decreased several times and
SD of GPER (Fig. 4c)
decreased one order of magnitude.
The number of the ``transient iterations'', i.e.
the number of the
skipped initial iterations
was further increased through