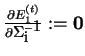


Next: Gaussova funkce
Up: Výpočet hodnot derivací chybové
Previous: Výpočet hodnot derivací chybové
Obsah
Algoritmus 3.4.1:
Vstup: RBF síť s 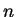 vstupními,
vstupními, 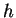 skrytými,
skrytými,  výstupními
neurony. Tréninková množina
výstupními
neurony. Tréninková množina
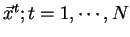
Výstup: Hodnoty
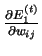 ,
,
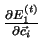 ,
,
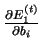 a
a
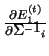 .
.
Značení:
-
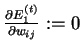 ,
,
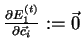 ,
,
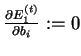 a
a
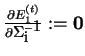
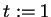
- Pro všechna
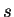 :
: 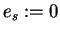
- Pro každou jednotku
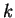
- spočti potenciál
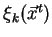 a členy
a členy 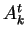 ,
,
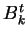 a
a 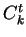
- spočti
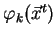 a
a

- pro všechna
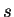 :
:
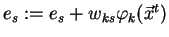
- Pro všechna
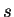 : v
: v 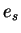 máme výstup
máme výstup 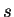 -té jednotky, odečteme od
něj
-té jednotky, odečteme od
něj 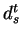 a získáme odchylku
a získáme odchylku 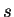 -té jednotky od požadovaného
výstupu.
-té jednotky od požadovaného
výstupu.
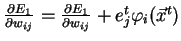
- Pro každou jednotku
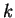
- Pokud
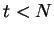 ,
, 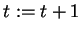 a přejdi k bodu 3.
a přejdi k bodu 3.
- Pro každou jednotku
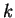
Petra Kudova
2001-04-19
![$\displaystyle A_k^t =
\frac{ [\vec{x}^t - \vec{c}^k]}{\parallel\vec{x}^t -
\vec{c}^k\parallel _{C_k}}$](img115.gif)
![$\displaystyle C_k^t =
\frac{[\vec{x}^t - \vec{c}^k][\vec{x}^t - \vec{c}^k]^T}{\parallel\vec{x}^t - \vec{c}^k\parallel _{C_k}}$](img117.gif)
![$\displaystyle A_k^t =
\frac{ [\vec{x}^t - \vec{c}^k]}{\parallel\vec{x}^t -
\vec{c}^k\parallel _{C_k}}$](img115.gif)
![$\displaystyle C_k^t =
\frac{[\vec{x}^t - \vec{c}^k][\vec{x}^t - \vec{c}^k]^T}{\parallel\vec{x}^t - \vec{c}^k\parallel _{C_k}}$](img117.gif)
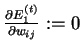 ,
,
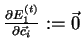 ,
,
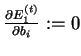 a
a