


Next: Poznámky
Up: Výpočet hodnot derivací chybové
Previous: Algoritmus 3.4.1:
Obsah
Vzorce pro výpočet derivace (3.4-3.7) předpokládají
pouze, že RBF jednotky počítají nějakou obecnou radiální funkci
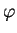 . Podívejme se nyní na nejrozšířenější případ, RBF jednotky s Gaussovo
funkcí, t.j.
. Podívejme se nyní na nejrozšířenější případ, RBF jednotky s Gaussovo
funkcí, t.j.
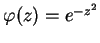 .
.
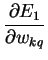 |
 |
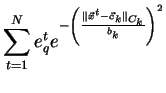 |
(3.9) |
 |
 |
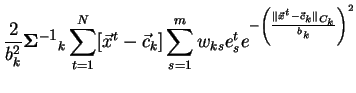 |
(3.10) |
 |
 |
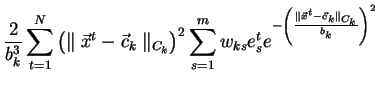 |
(3.11) |
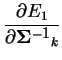 |
 |
![$\displaystyle -\frac{1}{b_k^2}\sum_{t=1}^{N}
[\vec{x}^t-\vec{c}^k][\vec{x}^t-\v...
...e^{-\left(\frac{\parallel \vec{x}^t - \vec{c}_k \parallel_{C_k}}{b_k}\right)^2}$](img149.gif) |
(3.12) |
Postup výpočtu je stejný jako v algoritmu 3.4.1, ale výpočet se
zjednodušší. Srovnáme-li vzorečky (3.4 - 3.7) se
vzorečky (3.9 - 3.12), vídíme, že místo členu
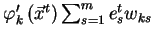 (viz také krok 6 algoritmu 3.4.1) nyní potřebujeme počítat
jednodušší člen
(viz také krok 6 algoritmu 3.4.1) nyní potřebujeme počítat
jednodušší člen
Tedy odpadá výpočet derivace
 a navíc
jednotlivé sčítance sumy počítáme již v kroku 5. Můžeme je tedy rovnou sčítat a
výpočet tohoto členu v kroku 6 odpadá.
a navíc
jednotlivé sčítance sumy počítáme již v kroku 5. Můžeme je tedy rovnou sčítat a
výpočet tohoto členu v kroku 6 odpadá.
Gaussova funkce má navíc tu výhodu, že svůj parametr umocňuje. Vždy stačí
spočítat jen hodnotu potenciálu na druhou a tedy při vyhodnocení vzdálenosti
nemusíme odmocňovat.



Next: Poznámky
Up: Výpočet hodnot derivací chybové
Previous: Algoritmus 3.4.1:
Obsah
Petra Kudova
2001-04-19
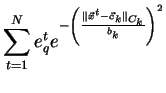
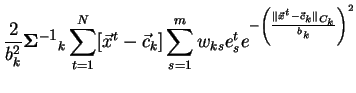
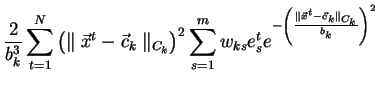
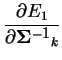
![$\displaystyle -\frac{1}{b_k^2}\sum_{t=1}^{N}
[\vec{x}^t-\vec{c}^k][\vec{x}^t-\v...
...e^{-\left(\frac{\parallel \vec{x}^t - \vec{c}_k \parallel_{C_k}}{b_k}\right)^2}$](img149.gif)
![]() (viz také krok 6 algoritmu 3.4.1) nyní potřebujeme počítat
jednodušší člen
(viz také krok 6 algoritmu 3.4.1) nyní potřebujeme počítat
jednodušší člen
