


Next: Genetické algoritmy
Up: Třetí fáze, problém nejmenších
Previous: Třetí fáze, problém nejmenších
Obsah
Problém nejmenších čtverců
Máme zadány matice 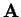 a
a  a hledáme takovou matici
a hledáme takovou matici
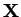 , že pro každou matici
, že pro každou matici 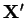 platí
platí
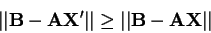 |
(4.25) |
Pokud neexistuje inverzní matice k matici  použijeme k řešení jednu
z následujících metod.
použijeme k řešení jednu
z následujících metod.
Moore-Penroseova pseudoinverse
Řešení spočteme
 |
(4.26) |
kde 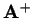 je pseudoinverze matice
je pseudoinverze matice  . Pseudoinverzí
matice
. Pseudoinverzí
matice 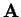 nazýváme takovou matici
nazýváme takovou matici 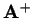 , pro kterou platí
, pro kterou platí
Existuje-li k matici A inversní matice, je rovna její pseudoinversi.
Pokud je matice
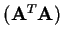 regulární, pak matice
regulární, pak matice
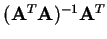 splňuje podmínky 1-4.
Tato matice bývá označována jako Moore-Penroseova pseudoinverse.
splňuje podmínky 1-4.
Tato matice bývá označována jako Moore-Penroseova pseudoinverse.
SVD rozklad
Pro každou matici
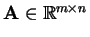 existují matice
existují matice 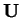 ,
,
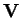 a
a  tak, že
tak, že
 |
(4.27) |
a
 a
a  je diagonální matice. Prvky diagonály
je diagonální matice. Prvky diagonály
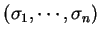 se nazývají singulární čísla matice
se nazývají singulární čísla matice 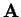 . Pokud je hodnost matice
. Pokud je hodnost matice
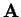 rovna
rovna  , pak
, pak
 jsou rovny
nule.
jsou rovny
nule.
Dosadíme-li za 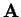 její SVD rozklad dostáváme
její SVD rozklad dostáváme
 |
(4.28) |
a tedy
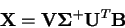 |
(4.29) |
kde
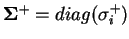 a
a
 , pro
, pro
 a
a
 , pro
, pro  .
.
G.H.Golub a C.Reinsch [10, str. 134-151] navrhli algoritmus na
výpočet SVD rozkladu. Nejprve upravíme matici na bidiagonální tvar a po té se
provádí vlastní rozklad. Redukce na bidiagonální tvar se provádí pomocí
Householderových transformací [8, str. 52-57]
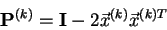 |
(4.30) |
 |
(4.31) |
tak, aby
 byla v horním bidiagonálním tvaru.
Matice
byla v horním bidiagonálním tvaru.
Matice  má stejná singulární čísla jako matice
má stejná singulární čísla jako matice 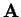 . Tedy
je-li
. Tedy
je-li
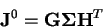 |
(4.32) |
pak
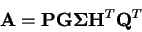 |
(4.33) |
tak, že
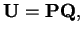
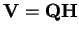 a
a
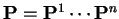 a
a
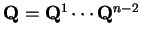 .
.
SVD rozklad bidiaogonální matice probíhá jako iterativní diagonalizace
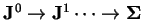 ,
kde
,
kde
 a
a
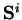 a
a 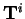 jsou transformační matice složené s Givensových
rotací [8, str. 49-51].
jsou transformační matice složené s Givensových
rotací [8, str. 49-51].
QR rozklad
B.Businger a G.H.Golub [10, str. 111-118] navrhli řešení problému
nejmenších čtverců pomocí Householderových transformací.
Máme matici
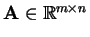 , kde
, kde 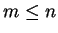 a hodnost matice
a hodnost matice
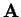 je
je 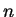 , a matici
, a matici  . Hledáme
. Hledáme 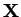 tak, aby
pro každou matici
tak, aby
pro každou matici 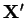 platilo
platilo
 |
(4.34) |
Platí, že
 , pokud
, pokud

Zvolíme  tak, aby
tak, aby
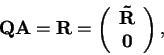 |
(4.35) |
kde
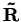 je horní trojúhelníková matice. Pak
je horní trojúhelníková matice. Pak
 .
.
Dekompozici lze realizovat pomocí Householderových transformací
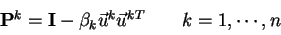 |
(4.36) |
Vektory  a parametry
a parametry  určíme tak, aby k-tá transformace
vynulovala v k-tém sloupci všechny prvky pod diagonálou.
určíme tak, aby k-tá transformace
vynulovala v k-tém sloupci všechny prvky pod diagonálou.
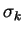 |
 |
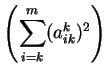 |
(4.37) |
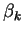 |
 |
 |
(4.38) |
 |
 |
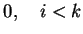 |
(4.39) |
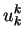 |
 |
 |
(4.40) |
 |
 |
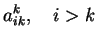 |
(4.41) |
Praktický výpočet probíhá iterativně. Po určení prvního řešení
 , položíme
, položíme
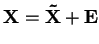 . Potom
. Potom
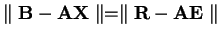 , kde
, kde
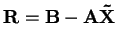 . Výpočet korekce
. Výpočet korekce
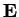 je snadný, neboť rozklad matice
je snadný, neboť rozklad matice 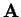 už máme.
už máme.



Next: Genetické algoritmy
Up: Třetí fáze, problém nejmenších
Previous: Třetí fáze, problém nejmenších
Obsah
Petra Kudova
2001-04-19
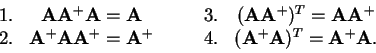
![]() její SVD rozklad dostáváme
její SVD rozklad dostáváme
![]() ,
kde
,
kde
![]() a
a
![]() a
a ![]() jsou transformační matice složené s Givensových
rotací [8, str. 49-51].
jsou transformační matice složené s Givensových
rotací [8, str. 49-51].
![]() , kde
, kde ![]() a hodnost matice
a hodnost matice
![]() je
je ![]() , a matici
, a matici ![]() . Hledáme
. Hledáme ![]() tak, aby
pro každou matici
tak, aby
pro každou matici ![]() platilo
platilo
![]() tak, aby
tak, aby
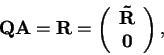
![]() a parametry
a parametry ![]() určíme tak, aby k-tá transformace
vynulovala v k-tém sloupci všechny prvky pod diagonálou.
určíme tak, aby k-tá transformace
vynulovala v k-tém sloupci všechny prvky pod diagonálou.
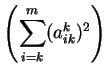
![]() , položíme
, položíme
![]() . Potom
. Potom
![]() , kde
, kde
![]() . Výpočet korekce
. Výpočet korekce
![]() je snadný, neboť rozklad matice
je snadný, neboť rozklad matice ![]() už máme.
už máme.