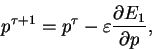


Next: Algoritmus 3.1.1:
Up: Gradientní učení RBF sítě
Previous: Gradientní učení RBF sítě
Obsah
Gradientní algoritmus
Uvažujeme-li pevnou tréninkovou množinu, pak funkce 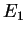 vyjadřuje chybu na
této množině v závislosti na konfiguraci sítě. Úkolem učení je nalézt takovou
konfiguraci, pro kterou je chyba sítě
vyjadřuje chybu na
této množině v závislosti na konfiguraci sítě. Úkolem učení je nalézt takovou
konfiguraci, pro kterou je chyba sítě 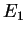 minimální.
minimální.
Algoritmus zpětného šíření pro vícevrstvé sítě perceptronů hledá pomocí
gradientního algoritmu minimum funkce  v prostoru parametrů.
v prostoru parametrů.
Algoritmus 3.1.1 popisuje použití gradientního algoritmu pro RBF
síť. Počáteční konfiguraci sítě zvolíme náhodně. V každém kroku algoritmu pak
upravíme všechny parametry podle
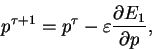 |
(3.1) |
kde 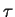 označuje diskrétní čas výpočtu,
označuje diskrétní čas výpočtu, 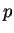 je konkrétní parametr a
je konkrétní parametr a
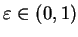 určuje rychlost učení. Tím posuneme konfiguraci ve směru tečného
vektoru funkce
určuje rychlost učení. Tím posuneme konfiguraci ve směru tečného
vektoru funkce  dolů o
dolů o  . Získáme tak novou konfiguraci, pro niž
je hodnota chybové funkce menší než chyba v předchozím bodě (
. Získáme tak novou konfiguraci, pro niž
je hodnota chybové funkce menší než chyba v předchozím bodě (
 ). To opakujeme dokud se nedostaneme do lokálního minima
funkce.
). To opakujeme dokud se nedostaneme do lokálního minima
funkce.
Subsections
Petra Kudova
2001-04-19
![]() v prostoru parametrů.
v prostoru parametrů.