Algoritmus 3.1.1:

1. $\tau := 0$
   Nastav náhodně $\vec{c}_k(0)$, $b_k(0)$, ${\bf\Sigma^{-1}_{k}}(0)$ a $w_{ks}(0)$ pro $s = 1, \cdots, m$ a $k = 1, \cdots, h$
2. $\tau := \tau + 1$
3. Spočti pro $s = 1, \cdots, m$ a $k = 1, \cdots, h$
   
   $$\begin{array}{ccccccc} \Delta \vec{c}_k &= & -\varepsilon ... ...-\varepsilon \frac{\partial E_1}{\partial w_{ks}} \end{array}$$
   
   

4. Uprav hodnoty parametrů pro $s = 1, \cdots, m$ a $k = 1, \cdots, h$
   
   $$\begin{array}{ccccccc} \vec{c}_k(\tau) &= & \vec{c}_k(\tau-1... ... w_{ks}(\tau) &= & w_{ks}(\tau-1) + \Delta w_{ks} \end{array}$$
   
   

5. Spočti chybu sítě, je-li dotatečně malá, skonči.
6. Přejdi k bodu 2.

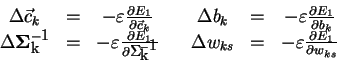
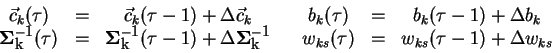
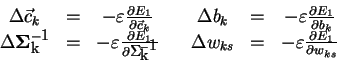
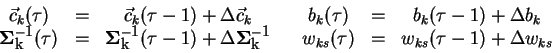
Algoritmus 3.1.1 představuje tzv. akumulované učení, kdy k adaptaci dochází po celém průchodu tréninkovou množinou. Hodnota chybové funkce závisí na všech tréninkových vzorech a k výpočtu hodnoty jejích derivací potřebujeme projít celou tréninkovou množinu. Nahradíme-li funkci $E_1$ parciální chybovou funkcí $E_1^t = \frac{1}{2} \sum_{s=1}^{m}(d_{s}^{(t)}-f_{s}^{(t)})^2$, jejíž hodnota závisí pouze na tréninkovém vzoru $\vec{x}^{(t)}$, můžeme adaptaci provádět po každém předložení tréninkového vzoru a snížíme nároky na paměť. Tento algoritmus však už neminimalizuje původní chybovou funkci a může zpomalovat konvergenci.