


Next: Výpočet hodnot derivací chybové
Up: Gradientní učení RBF sítě
Previous: Jiné varianty gradientního algoritmu
Obsah
Pro výpočet gradientního algoritmu potřebujeme vyjádřit derivace chybové funkce
podle všech hledaných parametrů, t.j. vah, středů, šířek a matice normy.
Derivaci chybové funkce
 |
|
 |
(3.3) |
podle jednotlivých parametrů snadno vyjádříme použitím pravidel o derivaci součtu a
složené funkce. Označme
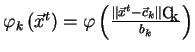 a
a
 .
.
Petra Kudova
2001-04-19


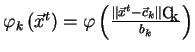 a
a
 .
.