Gradientní algoritmus

V prvním případě jsme použili gradientní algoritmus. Učená síť měla 50 jednotek, které měly adaptovatelné všechny parametry, včetně šířek a matic vah.

Výpočet jsme nechali běžet 10 000 iterací, hodnotu chybové funkce jsme zjišťovali po každé sté iteraci. Průměrný čas potřebný k provedení 100 iterací byl 101.5 s.

Experiment jsme provedli desetkrát. V prvních pěti případech jsme použili náhodné rozmístění středů a náhodné hodnoty vah blízké nule, náhodné hodnoty šířek blízké jedné a náhodné hodnoty matic vah blízké jednotkovým maticím. Dalších pět případů použilo jako středy náhodné vzorky z tréninkové množiny, nulové váhy, jednotkové šířky a matice vah. Druhá možnost nastavení vznikla během ladění a osvědčila se u některých testovacích úloh. V tomto případě dopadly obě skupiny zhruba stejně.

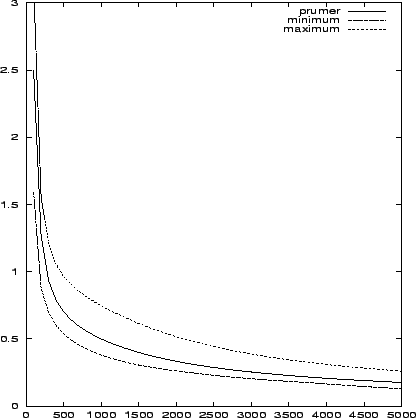
Obrázek 7.1 zobrazuje pokles chybové funkce během prvních 5 000 iterací. Zobrazen je průměr, minimum a maximum chybové funkce v provedených výpočtech.

**Obrázek 7.1:** Graf hodnot chyby sítě v závislosti na iteraci. Pro učení sítě o 50 jednotkách gradientním algoritmem.
$\begin{figure} \leavevmode \centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox {back50.eps}\end{figure}$

Během dalších 5 000 iterací je pokles chyby daleko pomalejší. Hodnoty jsou shrnuty v tabulce 7.1.

Tabulka 7.1: Hodnota chybové funkce v daném počtu iterací.

iterace	průměr	minimum	maximum
5000	0.1766	0.1297	0.2612
7500	0.1307	0.0820	0.1959
10000	0.1023	0.0562	0.1552

V tabulce 7.2 je uveden počet iterací potřebných k poklesu chybové funkce pod dané $\varepsilon$ .

Tabulka 7.2: Počet iterací potřebných k poklesu chybové funkce pod dané $\varepsilon$ .

$\varepsilon$	průměr	minimum	maximum
1	300	200	500
0.5	1100	600	2200
0.2	4300	3200	7400
0.1	-	6500	-

Gradientní algoritmus si s úlohou poradil. Funkce naučené sítě je na obrázku 7.2, průběh její chybové funkce na vstupním prostoru je znázorněn na obrázku 7.3.

**Obrázek 7.2:** Funkce sítě naučené gradientní metodou.
$\begin{figure} \leavevmode \centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox{sit50back.eps}\end{figure}$

**Obrázek 7.3:** Chybová funkce pro výsledek gradientního učení.
$\begin{figure} \leavevmode \centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox{error50back.eps}\end{figure}$