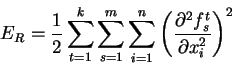


Next: Gradientní učení RBF sítě
Up: Učení RBF sítí
Previous: Učení RBF sítí
Obsah
Regularizace
Často klademe na zobrazení realizované sítí další požadavky. Naučená síť by
měla dávat rozumné výsledky i pro vstupy, které nejsou obsaženy v tréninkové
množině. Také situace, kdy funkce sítě prochází všemi body z tréninkové množiny
není vždy ideální, neboť v praxi tréninková množina často obsahuje šum.
Chris Bishop se v [1] zabývá řešením tohoto problému. K chybové
funkci přidává další člen 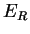 :
:
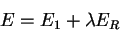 |
(2.13) |
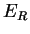 je zvolen tak, aby měl velké hodnoty pro funkce s velkou
oscilací. Parametr
je zvolen tak, aby měl velké hodnoty pro funkce s velkou
oscilací. Parametr 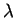 určuje míru vlivu tohoto regularizačního členu na
chybovou funkci.
Bishop volí
určuje míru vlivu tohoto regularizačního členu na
chybovou funkci.
Bishop volí 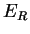 tak, že penalizuje funkce s velkou druhou derivací.
tak, že penalizuje funkce s velkou druhou derivací.
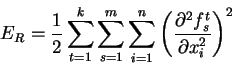 |
(2.14) |
Petra Kudova
2001-04-19
![]() :
:
![]() je zvolen tak, aby měl velké hodnoty pro funkce s velkou
oscilací. Parametr
je zvolen tak, aby měl velké hodnoty pro funkce s velkou
oscilací. Parametr ![]() určuje míru vlivu tohoto regularizačního členu na
chybovou funkci.
Bishop volí
určuje míru vlivu tohoto regularizačního členu na
chybovou funkci.
Bishop volí ![]() tak, že penalizuje funkce s velkou druhou derivací.
tak, že penalizuje funkce s velkou druhou derivací.