Algoritmus 4.1.2:

Vstup: $T = \{\vec{x}^t; t = 1, \cdots ,k\}$, počet reprezentantů $h$, kritérium ukončení výpočtu.
Výstup: $\vec{c}_j; j= 1, \cdots, h$

1. Rozmísti $\vec{c}_j$ náhodně.
2. Ke každému vektoru $\vec{x}^t \in T$ urči výherce kompetice $c$ a uprav $\vec{c}_c$ podle vzorce (4.7).
3. Spočti chybu, pokud je splněno dané kritérium, skonči.
4. Přejdi k bodu 2.

Výše uvedené algoritmy však řeší problém vektorové kvantizace jen tehdy, jsou-li vstupní hodnoty rozmístěny víceméně rovnoměrně v jedné konvexní oblasti. Podívejme se na obrázek 4.1.2. Vstupní data se vyskytují ve dvou čtercových oblastech, reprezentanty jsme při inicializaci umístili pouze do horní oblasti. Algoritmus 4.1.2 najde řešení zobrazené na obrázku 4.1.2. Jakmile je do dolní oblasti přitaženo několik nejbližších reprezentantů z horní oblasti, tito reprezentanti vyhrají všechny kompetice pro vstupy z dolní oblasti. To znamená, že žádný další reprezentat sem nebude přesunut. V nejhorším případě se může stát, že se v datech vyskytne oblast s pouze jedním reprezentantem, ačkoliv hustota výskytu vzorů v této oblasti může být vysoká.

Obrázek 4.1: Kohonenovo učení - počáteční rozmístění reprezentantů

Obrázek 4.2: Kohonenovo učení - výsledné rozmístění reprezentantů

K odstranění tohoto problému se používají různé heuristiky. Jednou z nich je tzv. radiální růst. Začneme s reprezentanty blízkými nule a tréninkovou množinou $T^{\prime} = \{ \beta\vec{x}^t; \vec{x}^t \in T \},$ kde $T$ je původní tréninková množina a $\beta$ je parametr blízký nule. Na začátku učení jsou tedy všechny vzory blízké všem reprezentantům. V průběhu učení zvyšujeme číslo $\beta$ a nakonec učíme původní data. Toto řešení je však časově náročné. Další řešení navržené Desienem(1988) je tzv. metoda lokální paměti. Vychází z předpokladu, že každý reprezentant by při stejné pravděpodobnosti měl zvítězit zhruba $1/h$-krát. Je-li tedy četnost výher nějakého reprezentanta příliš vysoká, vyřadíme ho na nějakou dobu ze soutěže. V samoorganizační síti Kohonenova učení přiřadíme každému neuronu dva parametry, relativní četnost výher $f$ a práh $b$. Učení pak probíhá tak, že po předložení tréninkového vzoru $\vec{x}^t$ určíme vítězný neuron $c$ a upravíme parametry $f$ a $b$ podle vzorce:

$$f_c^t = (1-\beta)f_c^{t-1} + \beta$$ (4.8)

$$f_j^t = (1-\beta)f_j^{t-1}, j \neq c$$ (4.9)

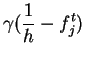$$b_j^t = \gamma (\frac{1}{h} - f_j^t)$$ (4.10)

Po té proběhne druhá kompetice

$$c = {\rm argmin}_{i=1,..h} \{ \parallel\vec{x}^t - \vec{w}_i\parallel - b_i\}$$ (4.11)

a vítěznému neuronu $c$ změníme váhy dle vzorce (4.7).

Výše uvedené algoritmy lze najít v [9]. Tam je také popsán složitější model samoorganizační sítě Kohonenova samoorganizační mapa, která vychází z  Kohonenova učení. Její neurony jsou však navíc uspořádány do nějaké topologické struktury, která určuje, které neurony spolu sousedí. Učení pak probíhá podobně jako Kohonenovo učení, ale spolu s vítěznými neuronem jsou navíc posunovány i všechny neurony z vítězova okolí.

Různými modifikacemi Lloydova algoritmu a dalšími metodami se zabývá [3], spíše však z hlediska kódování. Pro určení středů RBF jednotek postačí popsané metody, poslední z nich -- Kohonenovo učení --je zřejmě nejpoužívanější.