


Next: Kanonický genetický algoritmus
Up: Genetické algoritmy
Previous: Algoritmus 5.1.1:
Obsah
Učení RBF sítí pomocí GA
Učení neuronové sítě můžeme formulovat jako úlohu nalezení minima chybové
funkce v závislosti na parametrech sítě. K použití genetického algoritmu na
tuto úlohu potřebujeme zakódovat parametry sítě a dokázat ohodnotit takového
jedince odpovídající hodnotou účelové funkce.
Zakódování parametrů
Připomeňme si model RBF sítě z části 2.2. Vidíme, že síť je určena
svými RBF jednotkami a váhami spojů od těchto jednotek k výstupním
jednotkám. Každá jednotka je pak určena svými parametry - středem, případně
šířkou a maticí normy. Nabízí se tedy jednoduchá možnost zakódování parametrů
sítě do řetězce 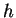 bloků, kde
bloků, kde 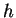 je počet RBF jednotek a každý blok obsahuje
zřetězení parametrů dané jednotky a vah spojů vedoucí z této jednotky do
výstupní vrstvy. Zakódování je zřejmé z obrázku 5.2.Určení počtu RBF
jednotek může být součástí učení. Délka jedince pak není konstantní.
je počet RBF jednotek a každý blok obsahuje
zřetězení parametrů dané jednotky a vah spojů vedoucí z této jednotky do
výstupní vrstvy. Zakódování je zřejmé z obrázku 5.2.Určení počtu RBF
jednotek může být součástí učení. Délka jedince pak není konstantní.
Obrázek 5.1:
Jedinec reprezentující neuronovou síť typu RBF. Blok reprezentující
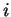 -tou RBF jednotku,
-tou RBF jednotku, 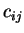 označuje souřadnici středu,
označuje souřadnici středu, 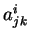 prvek
matice
prvek
matice 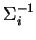 ,
, 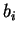 šířku a
šířku a 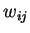 hodnotu váhy vedoucí k
hodnotu váhy vedoucí k 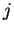 -té
výstupní jednotce
-té
výstupní jednotce
 |
Počáteční populace
První populaci vygenerujeme náhodně. Neznáme-li počet RBF jednotek, zvolíme
nějakou horní mez a každému jedinci určíme počet náhodně. Středy volíme náhodně
ve vstupním prostoru (t.j oblast výskytu tréninkových vzorů).
Účelová funkce
Hodnotu účelové funkce  pro daného jedince spočteme na základě hodnoty
chybové funkce sítě (viz část 2.4) určené tímto jedincem.
pro daného jedince spočteme na základě hodnoty
chybové funkce sítě (viz část 2.4) určené tímto jedincem.
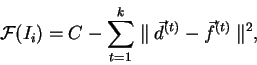 |
(5.1) |
kde
 je odhad maximální chyby, případně maximální chyba v dané
populaci.
V případě, že délka jedince není pevně dána, přidáme k účelové funkci další
člen, který bude penalizovat jedince s velkým počtem RBF jednotek.
je odhad maximální chyby, případně maximální chyba v dané
populaci.
V případě, že délka jedince není pevně dána, přidáme k účelové funkci další
člen, který bude penalizovat jedince s velkým počtem RBF jednotek.
Selekce
Použijeme tzv. ruletovou selekci. Představme si, že jedince vybíráme
pomocí ruletového kola, které je rozdělené na výseče odpovídající jednotlivým
jedincům. Velikost výseče odpovídá pravděpodobnosti 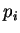 výběru daného jedince
výběru daného jedince
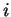 . Tuto pravděpodobnost určíme znormováním hodnot účelové funkce.
. Tuto pravděpodobnost určíme znormováním hodnot účelové funkce.
 |
(5.2) |
Selekci je navíc vhodné zkombinovat s tzv. elitářským mechanismem. Elita
je tvořená určitým počtem (např. 3-5%) nejlepších jedinců z dané populace,
kteří jsou reprodukováni do nové generace beze změny. Tak zajistíme, že maximum
hodnot účelové funkce neklesá.
Křížení
Použijeme jednobodové křížení. Vybrané jedince budeme označovat jako otce
a matku. Náhodně zvolíme body křížení pro otce i matku tak, aby ležely na
hranici bloků. V případě pevné délky jedince volíme bod křížení u otce i matky
na stejné pozici v řetězci. Nové jedince pak vytvoříme spojením první části
kódu otce s druhou částí kódu matky a naopak.
Mutace
U vybraného jedince náhodně zvolíme jeden blok a jeho hodnoty nebo některé
z jeho hodnot náhodně změníme.



Next: Kanonický genetický algoritmus
Up: Genetické algoritmy
Previous: Algoritmus 5.1.1:
Obsah
Petra Kudova
2001-04-19


