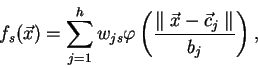


Next: Vážená norma
Up: Neuronové sítě typu RBF
Previous: RBF jednotka
Obsah
Model RBF sítě
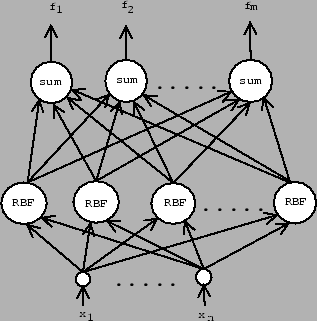
RBF síť je třívrstvá dopředná neuronová síť (viz obr. 2.2). První
vrstva obsahuje 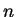 vstupních vstupních jednotek, které slouží pouze k předání
vstupních hodnot. Druhá -- skrytá -- vrstva obsahuje
vstupních vstupních jednotek, které slouží pouze k předání
vstupních hodnot. Druhá -- skrytá -- vrstva obsahuje 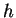 RBF
jednotek. Poslední -- výstupní -- vrstva je lineární a počet jejích jednotek
označme
RBF
jednotek. Poslední -- výstupní -- vrstva je lineární a počet jejích jednotek
označme  .
.
Obrázek 2.1:
Model RBF sítě
 |
RBF síť realizuje reálnou funkci
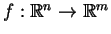 a to tak, že
nejprve vrstva RBF jednotek transformuje vstupní vektor
a to tak, že
nejprve vrstva RBF jednotek transformuje vstupní vektor
 na vektor
na vektor
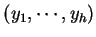 , a pak výstupní vrstva transformuje vektor
, a pak výstupní vrstva transformuje vektor
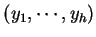 na vektor
na vektor
 .
.
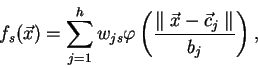 |
(2.5) |
kde 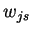 je váha spoje od j-té skryté jednotky do s-té výstupní jednotky.
Funkce sítě je tedy složením dvou funkcí, první nelineární funkce z
je váha spoje od j-té skryté jednotky do s-té výstupní jednotky.
Funkce sítě je tedy složením dvou funkcí, první nelineární funkce z
 do
do
 a druhé lineární funkce z
a druhé lineární funkce z
 do
do
 .
.
Budeme-li se dívat na síť jako na klasifikátor, můžeme říci, že úkolem první
vrstvy je transformovat vstupní vektor tak, aby jej bylo možno ohodnotit
lineární kombinací jeho nových souřadnic. Tímto problémem se v polovině 60. let
zabýval Cover [4, str. 237] a ukázal, že počet skrytých jednotek je
vhodné volit větší než je počet vstupních jednotek. To ukazují i výsledky
z praxe.



Next: Vážená norma
Up: Neuronové sítě typu RBF
Previous: RBF jednotka
Obsah
Petra Kudova
2001-04-19