Modifikace selekce a účelové funkce pro učení neuronových sítí

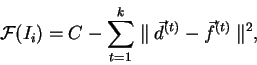
V části 5.2 popisujeme genetické operátory pro učení neuronových sítí. Připomeňme si výpočet hodnoty účelové funkce pro jedince reprezentujícího neuronovou síť ( 5.1).

$$\mathcal{F}(I_i) = C - \sum_{t=1}^k \parallel \vec{d}^{(t)} - \vec{f}^{(t)}\parallel^{2},$$

kde $C$ je odhad maximální chyby sítě.

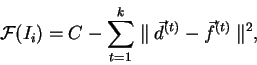
V praxi však volba této konstanty není jednoduchá. Jeli tato konstanta podstatně větší než hodnoty chyb příslušející k jedincům v populaci, ohodnocení jedinců v této populaci se příliš neliší a selekce pak neplní svůj účel. Pokud zvolíme hodnotu $C$ příliš malou, v populaci se může vyskytnout větší množství jedinců ze zápornou hodnotou účelové funkce. Protože záporná hodnota účelové funkce se neuvažuje, v praxi to znamená nulovou hodnotu. V populaci má pak skupina jedinců stejné (nulové) ohodnocení, ačkoliv jim odpovídající hodnoty chybových funkcí se liší.

Dá se očekávat, že jedinci v počátečních a několika dalších generacích budou odpovídat spíše špatně naučeným sítím a jejich chyba bude většinou vysoká. Naopak po delším běhu algoritmu budou převažovat lepší řešení, s malou chybou. Proto se v praxi často volí konstanta $C$ jako maximální chyba v dané populaci. Tím odstraníme výše uvedené problémy. Nevýhodou je však to, že účelová funkce pak ohodnocuje jedince pouze vzhledem k dané populaci. Nelze podle ní tedy usuzovat nic o vývoji výpočtu a rozhodovat o jeho ukončení.

Tento problém odstraníme jednoduchou úpravou genetického algoritmu. Jedinec bude ohodnocen pouze hodnotou chybové funkce odpovídající sítě.

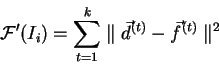$$\mathcal{F}'(I_i) = \sum_{t=1}^k \parallel \vec{d}^{(t)} - \vec{f}^{(t)}\parallel^{2}$$ (5.4)

Tedy čím menší ohodnocené, tím lepší řešení. Algoritmus tedy bude hledat místo maxima účelové funkce její minimum. Skončí po nalezení jedince z dostatečně malým ohodnocením a tento jedinec pak představuje řešení. Zbývá upravit operátor selekce tak, aby větší pravděpodobnost výběru měli jedinci s nižším ohodnocením. Tady opět využijeme hodnotu maximální chyby, ale v tomto případě stačí maximální chyba v dané populaci a tu známe. Pravděpodobnost výběru jedince $i$ spočteme jako

$$p_i = \frac{(1+\varepsilon )C-\mathcal{F}(I_i)}{N(1+\varepsilon )C - \sum_{j=1}^N \mathcal{F}(I_j)},$$ (5.5)

kde $N$ je počet jedinců v populaci, $C$ je maximální hodnota účelové funkce v dané populaci a $\varepsilon$ je kladné číslo blízké nule. Konstanta $\varepsilon$ zajišťuje, že i pravděpodobnost výběru nejhoršího jedince bude nenulová.