Genetické algoritmy

Poslední metodou použitou v prvním experimentu jsou genetické algoritmy. Nejprve jsme zkusili učit jedince s konstantní délkou, tedy opět sítě o 50 jednotkách. Populace měla 50 jedinců s elitou velikosti 2.

Experiment jsme provedli pětkrát s klasickým algoritmem a pětkrát s kanonickým algoritmem. Všechny výpočty jsme ukončili po 2500. generaci.

**Obrázek 7.6:** Graf hodnot chyby sítě v závislosti na generaci. Pro učení sítě o 50 jednotkách klasickým genetickým algoritmem.
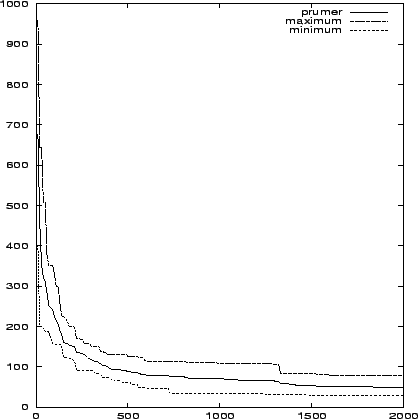
$\begin{figure} \leavevmode \centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox {gen50kl.eps}\end{figure}$

Výsledky byly poměrně špatné. Při použití klasického algoritmu síť dosáhla chyby v průměru 45.6, minimální chyba byla 28.53 a maximální 78.84. Průběh chybové funkce je vidět na obrázku 7.6. U kanonického algoritmu byla průměrná chyba v 2500. generaci 44.87, minimální 35.44 a maximální 60.24. Její průběh během výpočtu je zřejmý z obrázku 7.7. Kanonický algoritmus tedy dopadl jen nepatrně lépe. Když však porovnáme minimální a maximální chybu, zdá se, že u kanonického algoritmu jsou menší rozdíly mezi jednotlivými výpočty. Srovnání průběhu průměru chybové funkce kanonického a klasického algoritmu je na obrázku 7.8.

**Obrázek 7.7:** Graf hodnot chyby sítě v závislosti na generaci. Pro učení sítě o 50 jednotkách kanonickým genetickým algoritmem.
$\begin{figure} \leavevmode \centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox {gen50kan.eps}\end{figure}$

**Obrázek 7.8:** Srovnání poklesu chybové funkce u kanonického a klasického algoritmu.
$\begin{figure} \leavevmode \centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox {gen50cmp.eps}\end{figure}$

Dále jsme zkusili genetický algoritmus s proměnlivou délkou jedince. Jako maximální délku jsme zadali 50 jednotek. Provedli jsme opět deset výpočtů, z toho pět kanonickým algoritmem a pět klasickým algoritmem.

Výpočty běžely různě rychle v závislosti na velikosti jedinců v jednotlivých populacích. Výpočty jsme ukončili po 5 hodinách 59 minutách. Počet generací, které proběhli v jednotlivých výpočtech, a jim odpovídající výsledné chyby jsou zachyceny v tabulce 7.4.

V kanonickém algoritmu se prosadili kratší jedinci, proto běžel rychleji než klasický algoritmus a nakonec dosáhl lepších hodnot. Průběh průměrné chybové funkce obou algoritmů je zobrazen na obrázku 7.9

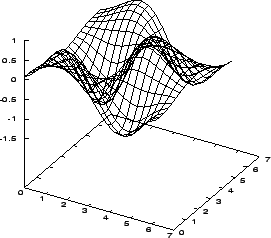
Ani tento experiment nedopadl nejlépe, zvláště když si uvědomíme poměrně velké rozdíly mezi jednotlivými výpočty. Kanonický algoritmus byl v tomto případě úspěšnější a to zejména díky využití kratších jedinců. Funkce sítě s chybou 14.02 (medián výsledných chyb kanonických výpočtů) je znázorněna na obrázku 7.10 a průběh její chybové funkce na vstupním prostoru znázorňuje obr. 7.11.

**Obrázek 7.9:** Vývoj chybové funkce u výpočtu s proměnlivým počtem jedinců.
$\begin{figure} \leavevmode \centering\centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox {gendif50.eps}\end{figure}$

Tabulka 7.4: Situace spuštěných výpočtů v čase 5h 49min

	Klasický algoritmus			Kanonický algoritmus
	Iterace	Chyba	Délka	Iterace	Chyba	Délka
1	2330	27.18	22	8230	21.50	14
2	1860	23.62	31	10260	16.18	9
3	2520	21.66	25	12900	9.43	11
4	3710	22.10	32	9300	11.43	11
5	1570	20.69	36	15530	14.02	10

**Obrázek 7.10:** Funkce sítě naučené genetickým kanonickým algoritmem, síť má 10 jednotek a chybu 14.02.
$\begin{figure} \leavevmode \centering\centering\epsfxsize =0.6\textwidth \epsfysize =0.3\textheight \epsfbox {sit50gendif.eps}\end{figure}$

**Obrázek 7.11:** Chybová funkce sítě z obrázku 7.10.
$\begin{figure} \leavevmode \centering\centering\epsfxsize =0.6\textwidth \epsfysize =0.3\textheight \epsfbox{error50gendif.eps}\end{figure}$