Genetické algoritmy

Použili jsme populaci 50 jedinců a pustili jsme pětkrát klasický algoritmus a pětkrát kanonický algoritmus. Do elity byli v obou případech vybíráni dva nejlepší jedinci. Všichni jedinci měli stejnou délku, 16 jednotek.

Oba výpočty jsme nechali běžet 5 000 generací, průměrný čas potřebný na 100 generací byl v obou případech 38.45 s.

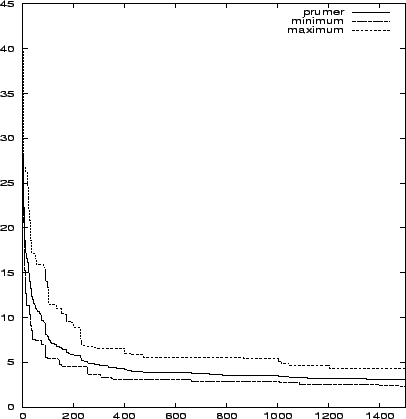
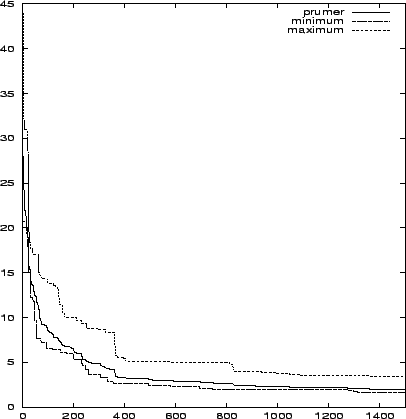
Na obrázcích 7.17 a 7.18 je vidět průběh minima, maxima a průměru chybové funkce v závislosti na generaci. Srovnání průměrného výpočtu kanonického a klasického algoritmu je pak na obrázku 7.19, kde vidíme, že kanonický výpočet si vedl o něco lépe.

Funkce sítě naučené kanonickým genetickým algoritmem je na obrázku 7.20, obrázek 7.21 znázorňuje průběh její chybové funkce.

**Obrázek 7.17:** Graf hodnot chyby sítě v závislosti na generaci. Pro učení sítě o 16 jednotkách nekanonickým genetickým algoritmem.
$\begin{figure} \leavevmode \centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox {gen16.eps}\end{figure}$

**Obrázek 7.18:** Graf hodnot chyby sítě v závislosti na generaci. Pro učení sítě o 16 jednotkách kanonickým genetickým algoritmem.
$\begin{figure} \leavevmode \centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox {can16.eps}\end{figure}$

**Obrázek 7.19:** Srovnání kanonického a klasického genetického algoritmu.
$\begin{figure} \leavevmode \centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox {compare16gen.eps}\end{figure}$

Tabulka 7.9: Průběh chyby v pozdějších generacích.

	počet generací	průměr	minimum	maximum
klasický	2000	2.833	1.412	4.125
algoritmus	3000	2.482	1.412	3.422
	5000	2.070	1.396	2.809
kanonický	2000	1.658	1.455	2.275
algoritmus	3000	1.298	1.192	1.747
	5000	1.064	0.822	1.640

Tabulka 7.10: Počet generací nutných pro pokles chyby pod dané $\varepsilon$ .

	Kanonický alg.			Klasický alg.
$\varepsilon$	průměr	minimum	maximum	průměr	minimum	maximum
20	20	19	27	9	9	32
10	68	48	168	76	34	173
5	260	234	813	258	148	1014
2	1511	832	2342	-	1660	-
1	-	3734	-	-	-	-

**Obrázek 7.20:** Funkce sítě naučené kanonickým genetickým algoritmem.
$\begin{figure} \leavevmode \centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox {sit16gen.eps}\end{figure}$

**Obrázek 7.21:** Chybová funkce sítě z obr. 7.20.
$\begin{figure} \leavevmode \centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox {error16gen.eps}\end{figure}$

Dalších pět výpočtů jsme provedli s kanonickým algoritmem s proměnlivou délkou jedince. Výpočet běžel 5 000 generací a průměr výsledných chyb je 3.655. Minimální dosažená chyba byla 1.4947 a maximální 13.3641. Tyto hodnoty už jsou přijatelné.

Průměrný čas na výpočet 100 generací je 8.34 s, je však závislý na délce jedinců v dané populaci, proto se během výpočtu mění.

Průběh chybové funkce je znázorněn na obrázku 7.22. Na obrázku 7.23 pak vidíme jak se mění délka nejlepšího jedince v průběhu výpočtu. Na začátku výpočtu jsou sítě v populaci spíše náhodné a menší sítě mají spíše menší hodnotu chybové funkce. Proto délka nejdříve prudce klesne na malé hodnoty. Během výpočtu se pak pomalu prosazují i delší jedinci, ale nárůst délky je velice pozvolný.

**Obrázek 7.22:** Chybová funkce, kanonický genetický algoritmus s proměnlivou délkou jedince.
$\begin{figure} \leavevmode \centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox {gendif16.eps}\end{figure}$

**Obrázek 7.23:** Délka nejlepšího jedince v průběhu prvních iterací.
$\begin{figure} \leavevmode \centering\epsfxsize =0.8\textwidth \epsfysize =0.4\textheight \epsfbox {delka.eps}\end{figure}$

Tabulka 7.11: Počet generací nutných pro pokles chyby pod dané $\varepsilon$ . Kanonický algoritmus s proměnlivou délkou jedince.

$\varepsilon$	průměr	minimum	maximum
20	9	9	23
10	196	135	-
5	865	334	-
2	-	1566	-