Poznámky

Uvedli jsme gradientní algoritmus pro učení obecné RBF sítě. Uvažovali jsme RBF síť, která má RBF jednotky určené středem, šířkou a maticí normy. Algoritmus lze samozřejmě použít pro RBF síť, jíž některý z těchto parametrů chybí. Například uvažujeme-li RBF síť, jejíž jednotky nemají adaptovatelnou šířku, v příslušných vzorcích nahradíme šířku jedničkou. Stejně tak RBF síť používající euklidovskou normu odpovídá RBF síti, kde matice norem jsou jednotkové.

Další možností je RBF síť, která používá pro všechny jednotky jednotnou normu. Norma pak není parametrem RBF jednotky, ale RBF sítě. Adaptuje se stejně jako ostatní parametry, potřebnou derivaci spočteme jako

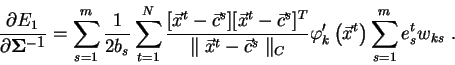$$\frac{\partial E_1}{\partial {\bf\Sigma^{-1}}} = \sum_{s=1}^... ... \varphi_k'\left(\vec{x}^t\right)\sum_{s=1}^m e_s^{t}w_{ks}\ .$$ (3.13)

Srovnáme-li vzorec (3.13) a (3.7), vidíme že tuto derivaci můžeme spočítat jako sumu derivací (3.7).